2025/09/20 Sat
活動
隊員Gのセントルシア日記_37 〜Difference in How to Teach Math〜

私の協力隊活動におけるミッションは「数学の学力向上」です。配属先がカレッジですので、まずは目の前にいる学生達の学力アップに取り組んでいます。今回は、セントルシアと日本における数学の教え方の相違点をご紹介して、読者の皆さんと共に「学力向上」について考えてみたいと思います。
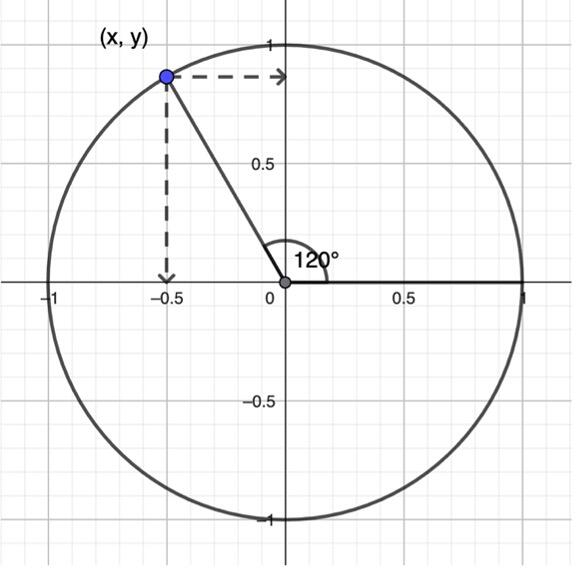
まずは、90°以上の角度の三角関数の求め方です。定義は、単位円(原点を中心とする半径1の円)上の点のx座標がコサイン、y座標がサインです。日本では、この定義に戻り、単位円を利用して、三角関数の値を求めます。ところが、セントルシアでは、例えば、120°の三角関数であれば、まずは参照角と呼ばれる補角60°の三角比の値を一旦求めます。そして、120°は第2象限の角だから、サインはプラス、コサインはマイナスと符号を決定するのです。もちろん、間違いではありませんが、定義を離れてしまうところに、リスクが潜むような気がしてなりません。また、三角方程式を解く際も、日本であれば、単位円を利用しますので、ビジュアル的なイメージをもちながら、解に辿り着くことができます。ところが、セントルシアでは、一旦符号を無視して、とにかく参照角(90°未満の角)の三角比を求めることにエネルギーが注がれるのです。そもそも、セントルシアでは、「三角関数の値は、関数電卓が計算してくれるもの。」「三角方程式の解も、逆関数を使えば、関数電卓が計算してくれる。」と考えられているようです。最低限度のスキル(参照角の三角比)さえ身につければ、「電卓にできる計算は電卓に任せて、我々は思考すること、判断すること、表現することに集中しましょう。」というフィロソフィーなのです。確かに、試験問題を見ても、実用的な場面設定が多く、「覚える」「理解する」よりも、「応用する」「分析する」「評価する」「創造する」という認知領域に力点が置かれていることは明らかなのです。
次に、標準正規分布における確率の求め方です。平均0、標準偏差1の標準正規分布には、確率変数Zの値に対して、標準正規分布表と呼ばれる確率計算のための表が用意されています。標準偏差±1σの範囲(-1<Z<1)に全体の約68%のデータが含まれており、±2σの範囲(-2<Z<2)には全体の約95%のデータが含まれている、という有名な確率計算を導くことのできる表です。セントルシアでは、正のZ値に対して左側確率を与える標準正規分布表が使われています。そして、なんと
Z値が正の場合の右側確率については、P(Z>1.5) = 1 - P(Z<1.5)
Z値が負の場合の右側確率については、P(Z>-1.2) = P(Z<1.2)
という式変形が公式として紹介されるのです。日本であれば、画像にあるように、簡単な絵を描いて、式変形の必要性をイメージした上で、標準正規分布表を参照するところです。というのも、標準正規分布表は他にも、正のZ値に対して、右側確率を与えるものがあれば、左側半分だけの確率を与えるものもあるのですから。残念ながら、一般的な関数電卓に確率計算の機能はありませんので、「それならば、公式に機械的に当てはめる」というのが、セントルシア的な発想のようです。やはり、計算を工夫すること自体にあまり興味はないのです。
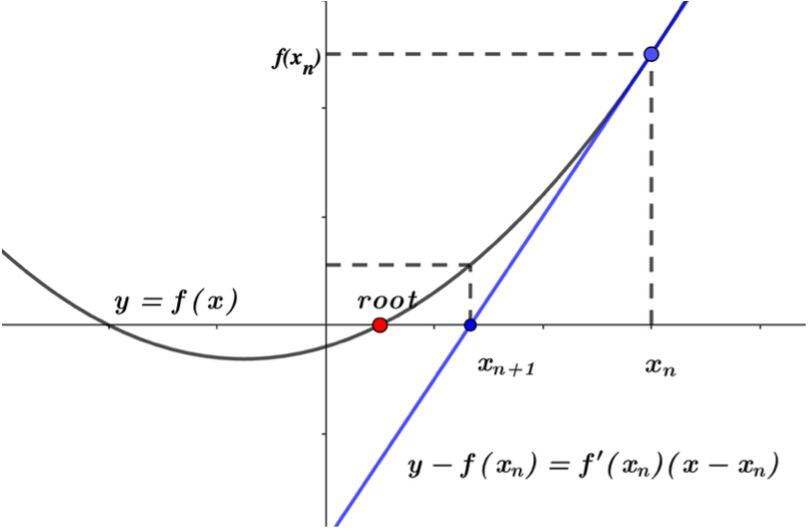

最後は、ニュートン・ラプソン法です。二次関数であれば、x切片(root)は二次方程式の解として求めることが可能です。しかし、一般的な関数のrootは、計算では求められないケースがありますので、近似的に求めるためのアルゴリズムが用意されているのです。日本であれば、漸化式を導くこと自体に力点が置かれ、近似値に関心が集まることは、余りありません。ところが、セントルシアでは関数電卓が手元にありますので、反復計算を行なって、rootの近似値を力技で求めてしまおうとするのです。関数値がゼロとなる場所に対して、大いに興味が示されており、まさに理科的な発想であると言えます。もしかすると、旧宗主国・英国が生んだ大巨人への敬慕なのかもしれませんね。
関数電卓のある、なしで、これほどまでに教育が異なるのか、というのが正直な私の感想です。しかし、セントルシアにおいて、関数電卓が理想的な使われ方をして、実用場面において「応用する」「分析する」「評価する」「創造する」力が育まれているかというと、疑問が残ります。率直に言えば、「関数電卓の誤った使い方が、学力向上の妨げになっているかもしれない。」という見方をせざるを得ないのです。日本でも、タブレットやPCが授業に導入される際に、使い方指導が話題になりました。タブレットやPCと同様に、関数電卓があれば様々な可能性が広がりますので、関数電卓自体を否定する気持ちは全くありません。ただし、関数電卓を正しく使うためのガイドラインは整備されなければならない、と強く思うのです。セントルシアの子ども達の学力向上のために。
SHARE





