閉じる

　数学の学習には、抽象的な概念が持ち込まれます。例えば、同じ文字でも、「文字定数」と「文字変数」は異なります。円周率（定数）を表すπには、3.14159……という値が予め入っていますが、変数を表すxには、さまざまな値が入るのです。また、「方程式」と「関数式」も全く違うものです。方程式2x−3＝０のxは1.5ですが、独立変数xと従属変数yの関係を表す関数式y＝2x−3において、xはさまざまな値を取るのです。そして、「〜に近づく」という「極限」の概念は、単なる「代入」とは異なり、新たに微積分の世界へと私たちを誘ってくれるのです。

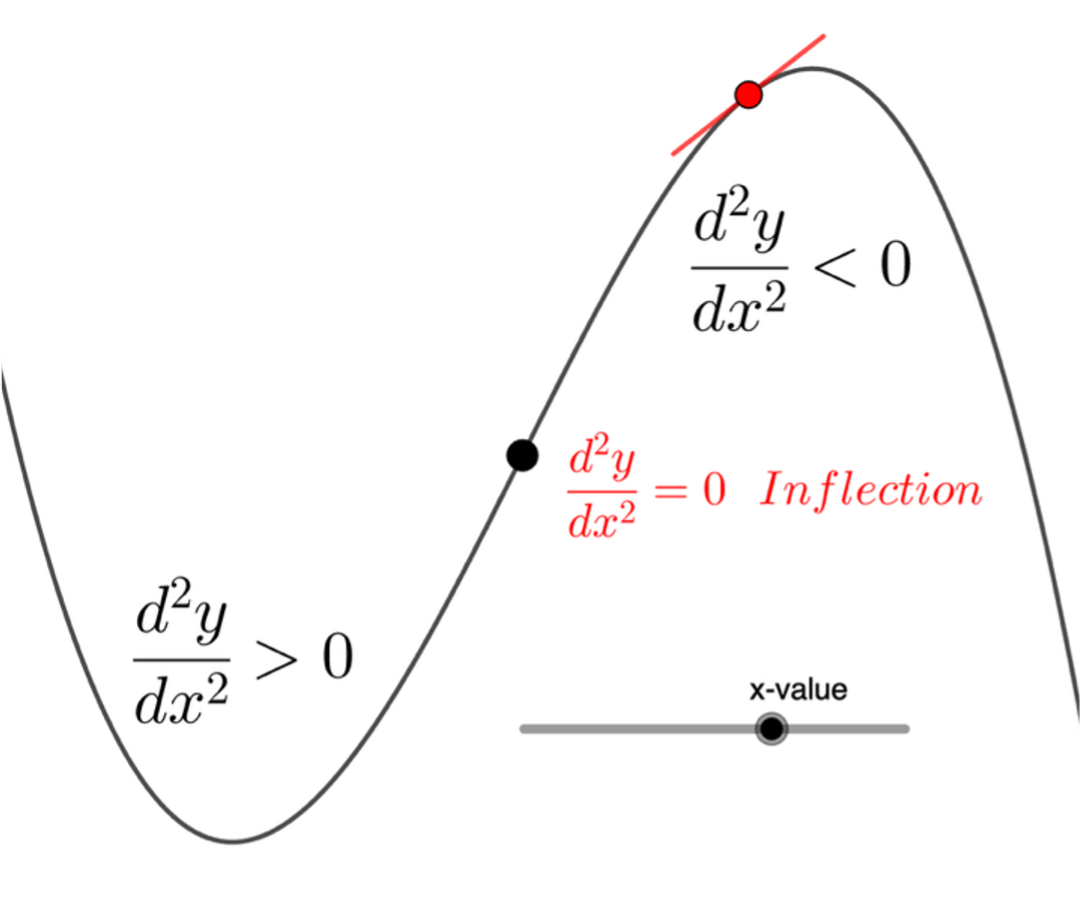
　さて、これまで何度もお話ししてきたように、セントルシアの学生たちは関数電卓を持っています。そして、心が折れるような計算にも果敢にチャレンジしてくれます。例えば、関数の変曲点であることを示すには、第2次導関数の符号の変化を確認するのですが、実際に近隣の第2次導関数の値を計算して、符号が変化している事実を訴えようとするのです。（電卓を持たない日本の学生なら、第2次導関数のグラフが描ける場合は、そのグラフから符号の変化を読み取ります。）目にみえる具体的な事象を追求しようとするエネルギー・レベルは高く、おそらく日本人の学生たちも舌を巻くことでしょう。

閉じる

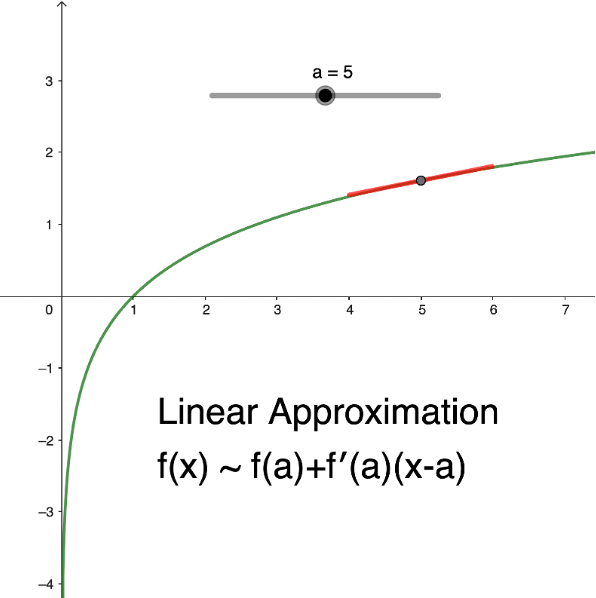
しかし逆に、目に見えない抽象的な概念の理解に関しては、苦手意識をもつセントルシアの学生が少なくないように思われます。例えば、「関数の1次近似」については、公式の「f(x) = f(a)+f’(a)(x-a)」を覚えて、具体的な1次近似式を求めることにはとても一生懸命です。しかし、この公式が「曲線を、直線で近似的に表す」ものであることを理解している学生は少ないのです。すなわち、公式の本質的な意味（抽象的な概念）を理解することなく、数学を学んでいるのです。「これでは、数学の本当の楽しさや面白さは伝わらない」と、私は思い悩みました。そして、思案の末に、彼らの抽象概念の理解を助けるビジュアル教材の開発を志すことにしたのです。先ほどの、「関数の1次近似」に関しては、Geogebraというアプリを使って次のようなモデル教材を作りました。

https://www.geogebra.org/classic/h3usrf8h

閉じる

　今回の日記では、代表的なビジュアル教材をいくつか紹介したいと思います。まずは、2次関数の2次の係数a、1次の係数b、定数項c の値を変えることによって、放物線の形がどうのように変化するかを理解するための教材。「グラフ」が単なる「絵」でないことをしっかり伝えるために、ビジュアルに訴えました。

https://www.geogebra.org/classic/knpgbdbx

ドラッグすることによって、a、b、cそれぞれの値を変えることができますので、放物線の形が実際、どのように変化するかを体験してみて下さい。学生たちが、ビジュアル教材を通して、抽象概念をハンズ・オン体験する、というところを狙っています。

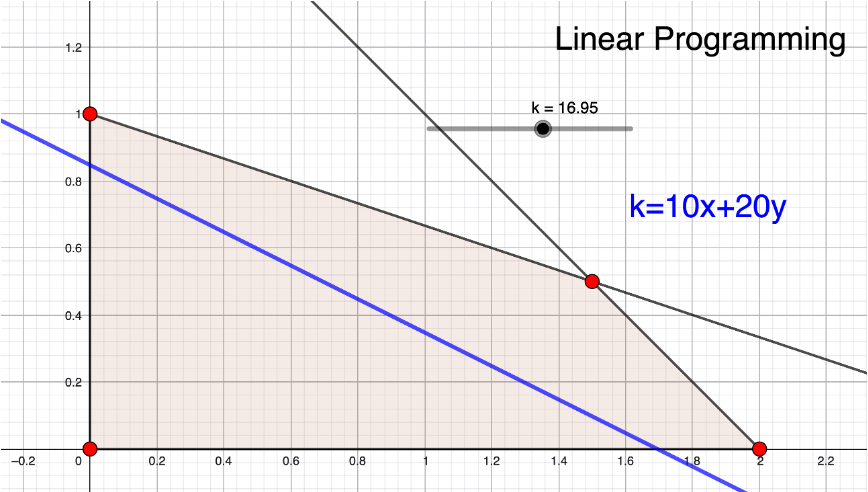
　続いては、線形計画法の教材です。「10ドルの商品Aをx千個、20ドルの商品Bをy 千個を製造して販売するときに、売上げを最大にするには、商品A、Bをそれぞれ何千個製造すれば良いか」を考える問題です。（ただし、「製造個数x、yについては、機械の性能上、さまざまな制約を受けるので、座標平面において色塗りした範囲内の値しか取ることはできません。」）

https://www.geogebra.org/classic/pzw83rrw

k＝10x＋20y とおいて、売上げk千ドルがどのように変化するかを見極めるためのビジュアル教材です。ドラッグすることによって、kの値を変えることができますので、kの最大値を実際にハンズ・オン体験してみて下さいね。

　最後に、「放物線が焦点をもつ」ことを理解するために、「パラボラ・アンテナが電波を焦点に集める」様子のモデルを作りました。

https://www.geogebra.org/classic/tye8jfdy

電波がやってくる位置sを変えることができます。ドラッグしてsの値を変えて、どこからやってくる電波も、必ずパラボラ・アンテナ（放物線）の焦点に集められることを、ハンズ・オンで体験してみて下さい。電波が増幅される仕組みですね。

　今後も、絶えず、「学生たちの抽象概念の理解を助けるために、何ができるか」という問いに、しっかりと向き合っていきたい、と考えています。